Make Realistic Fake Blood Without a Cleanup Surprise
Mix a glossy prop-only fake blood batch, choose safer products for skin and costumes, and test cleanup before Halloween night.
Convert from base 16 to base 10
Hexadecimal and decimal systems
The hexadecimal system has 16 digits. The digits 1 through 9 are the same as in the decimal system, then the decimal numbers 10 through 15 are replaced by the letters A, B, C, D, E, and F of the English alphabet.
The decimal system (also known as the base 10 system) is a standard system for representing integers and non-integer numbers (decimal numbers). It is an extension for non-integer numbers of the Hindu-Arabic numeral system.
How to convert base 16 to base 10
Hex is a base 16 number system and decimal is a base 10 number system. Sometimes, we need to know the decimal equivalent of a hexadecimal number.
Here are the steps to convert from base 16 to base 10:
- Get the decimal equivalent of the hexadecimal digit from the table.
- Multiply each digit by the power of 16 (the exponent corresponds to the digit's position, the rightmost digit corresponds to the 0 position). For example, in 7DE, the E position is 0, the D position is 1, and the 7 position is 2.
- Calculate the sum of all multiplications.
Here is an example:
7DE is a hexadecimal number
- 7DE = (7 * 162) + (13 * 161) + (14 * 160)
- 7DE = (7 * 256) + (13 * 16) + (14 * 1)
- 7DE = 1792 + 208 + 14
7DE = 2014 (in decimal)
Example of converting from base 16 to base 10:
- (1D9)16 = (473)10
- (80E1)16 = (32993)10
- (10CE)16 = (4302)10
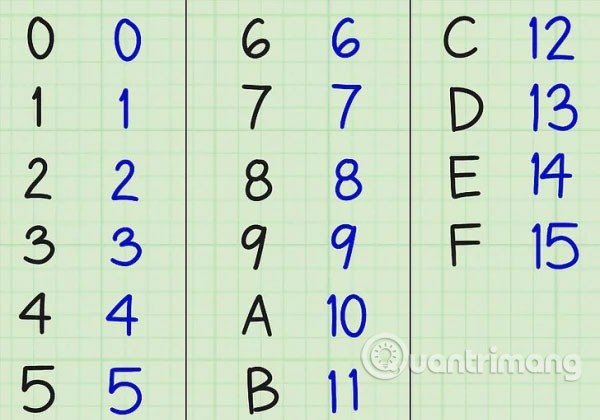
Conversion table from base 16 to base 10
| Hexadecimal system | Base 10 system |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
See also:
Kawaii Halloween Decor Without Gore or Jump Scares
Create a gentle Halloween look with pastel colors, friendly ghosts, easy no-carve accents, and practical safety tips for your home.
Desk Decorating Ideas for a Spooky Office Cubicle
Create a spooky office cubicle with Halloween desk decor ideas that keep your workspace usable, tidy, and mindful of workplace safety.
Pop Culture Costume Ideas That Will Dominate Halloween 2026
Plan a recognizable Halloween 2026 look with pop culture costumes inspired by Spider-Man, Supergirl, Toy Story 5, Moana, Mario, and Wednesday.
Leftover Halloween Candy and Pumpkins: What to Do Next
Sort leftover Halloween candy safely, share or repurpose sealed treats, and choose food use or compost for pumpkins based on their condition.
What Not to Wear: A Guide to Professional Workplace Halloween Etiquette
Compare workplace Halloween costume choices by respect, dress code, mobility, and safety—and learn when a subtle accessory or a policy check is the better option.
Couples Costume Ideas for 2026: Iconic Pairs and Clever Tropes
Find a couples costume that fits your style, budget, and comfort level, from Addams Family classics to original inside-joke duos.
Last-Minute High School Halloween Costumes That Take 5 Minutes
Need a last-minute high school Halloween costume? Compare 10 easy closet-based ideas by prep time, comfort, school-day practicality, and simple safety checks.
When to Start Decorating for Halloween in 2026
Use a simple 2026 Halloween decorating timeline for indoor décor, outdoor displays, and fresh pumpkins, with practical adjustments for weather and events.
5 Halloween Cocktails That Are Easy to Serve at Your 2026 Bash
Mix five vivid, approachable Halloween cocktails with measured recipes, simple prep tips, and an alcohol-free option for your party guests.