Formula for calculating area of ​​rhombus, perimeter of rhombus

Let's review and memorize the formula for calculating area, perimeter of a rhombus and diagonal of a rhombus in the article below.

Table of Contents

• 1. Formula for calculating the area of ​​a rhombus
  • Formula for calculating the area of ​​a rhombus based on the base and height
  • Formula for calculating the area of ​​a rhombus based on the triangle formula (If you know the angle of the rhombus)
• 2. Formula for calculating the perimeter of a rhombus
• 3. What is a rhombus?
  • Properties of rhombus
• 4. Example of calculating area and perimeter of rhombus

1. Formula for calculating the area of ​​a rhombus

The area of ​​a rhombus is measured by the size of the surface area, which is the visible flat part of the rhombus.

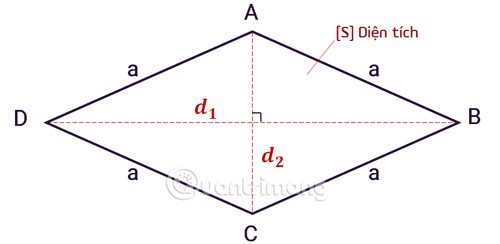
Formula for calculating the area of ​​a rhombus based on the base and height

The area of ​​a rhombus is equal to half the product of the lengths of the two diagonals , the formula is as follows:

In there:

• Sis the area of ​​the rhombus.
• d1and d2are the two diagonals of a rhombus.

Example of calculating the area of ​​a rhombus.

Lesson 1: There is a rhombus-shaped piece of cardboard with two intersecting diagonals of lengths 6 cm and 8 cm respectively. What is the area of ​​the rhombus-shaped piece of cardboard?

Applying the method of calculating the area of ​​a rhombus, we have d1 = 6 cm and d2 = 8 cm. We put it into the formula and get the following result:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Formula for calculating the area of ​​a rhombus based on the triangle formula (If you know the angle of the rhombus)

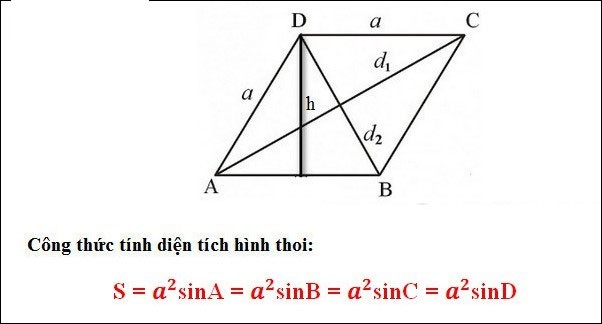
In which: a: side of rhombus

Example 1 : Given rhombus ABCD, with rhombus edge = 4cm, angle A = 35 degrees. Calculate the area of ​​rhombus ABCD.

Solution: Applying the formula, we have a = 4, angle = 35 degrees. We substitute into the formula as follows:

S = a2 x sinA = 42 x sin(35) = 9.176 (cm2)

2. Formula for calculating the perimeter of a rhombus

The perimeter of a rhombus is calculated by adding the lengths of the lines surrounding the shape, which is also the line surrounding the entire area.

To calculate the perimeter of a rhombus, we calculate the sum of the lengths of the four sides. The specific formula is as follows:

In there:

• Pis the perimeter of a rhombus.
• ais the length of the side of the rhombus.

For example: Given a rhombus ABCD with equal side lengths and 7 cm. What is the perimeter of this rhombus?

According to the formula for calculating the perimeter of a rhombus introduced above, we have a = 7 cm. Thus, the perimeter of rhombus ABCD will be calculated as follows:

P (ABCD) = ax 4 = 7 x 4 = 28 cm

3. What is a rhombus?

A rhombus is a quadrilateral with four equal sides. It is a parallelogram with two adjacent sides equal or a parallelogram with two diagonals perpendicular to each other.

Properties of rhombus

• 2 equal opposite angles
• 2 diagonals are perpendicular to each other and intersect at the midpoint of each line
• The two diagonals are the bisectors of the angles.

In this article, Quantrimang.com will reintroduce effective formulas for calculating the area and perimeter of a rhombus for your study and work.

4. Example of calculating area and perimeter of rhombus

Example 1: 

Given rhombus ABCD with side AD = 4m, angle DAB = 30 degrees. Calculate the area of ​​rhombus ABCD.

Prize:

Because ABCD is a rhombus, the triangles formed are isosceles triangles. Let I be the midpoint of the two diagonals, so AI is perpendicular to BD, angle IAB = 15 degrees.

Therefore, AI = AB. cos IAB = 4. Cos 15 = 3.84m.

Consider the right triangle ABI, according to the Pythagorean theorem, we have:

BI2= AB2- AI2= 1.25m

So BI = 1.1m

AC = 2. AI = 7.68m

BD = 2. BI = 2.2m

Based on the formula for calculating the area of ​​a rhombus, we have the area of ​​a rhombus ABCD = ½ . AC . BD = 8.45(m2)

Example 2: Given a rhombus with a side length of 6cm and one of its angles has a measure of 60°, calculate the area of ​​the rhombus.

With these facts, you will not have any basis to calculate the area of ​​a rhombus. You will have to rely on the properties of rhombuses, properties of equilateral triangles , and how to calculate the sides in a right triangle to calculate the diagonal of the rhombus. The steps are as follows:

Step 1: Draw a picture and note the known facts.

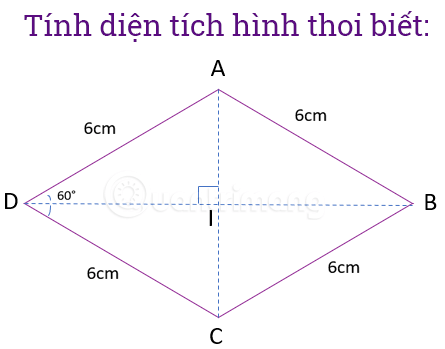
Step 2: Applying the properties of a rhombus we have:

, diagonal AC is the bisector of angle A, so the angle will be equal to 1/2 angle and equal to 60°. (The sum of the interior angles of a quadrilateral is 360°, the sum of the interior angles of a triangle is 180°). Thus, triangle ADC will be an equilateral triangle => side AC is 6cm. I is the midpoint of AC => AI=3cm.

Step 3: Calculate the length of DI

Triangle DIA is right-angled at I, side DI will be calculated as follows:

=> cm

Step 4: Calculate the area of ​​rhombus ABCD:

Example 3: Given rhombus ABCD with side length 13cm, two diagonals intersect at H.

Calculate the area of ​​rhombus ABCD knowing that BH is one and a half times AH.

Solution:

ABCD is a rhombus, so AH is perpendicular to BH at H, then triangle ABH is right-angled at H.

Let BH= 2a, then AH =3a.

According to the Pythagorean theorem we have: AH²+ BH²= AB² ⇒9a²+4a²=13 ⇒13a²=13 ⇒a=1

Therefore AH= 3cm, BH= 2cm or AC= 6 cm, BD= 4cm

The area of ​​the rhombus is: S = 6.4/2= 12cm².

Example 4 :

Given rhombus MNPQ, angle A = 30o, perimeter = 20m, midpoint of diagonal is I. What is the area of ​​rhombus MNPQ?

Solution

The length of the side of the rhombus is a = P : 4 = 20 : 4 = 5m

Because the triangles created by rhombuses are all isosceles triangles, the triangle created from the midpoint of diagonal I, points M, N will be created by angle IMN = 15o

Length of half diagonal MI = MN x cos IMN = 5 x cos150 = 4.8m

Applying the Pythagorean theorem in right triangle MNI we have: NI = 1.4m

Diagonal length NQ = 2 x NI = 2 x 1.4 = 2.8m

The area of ​​rhombus MNPQ is S = 2 x ½ x NQ x MI = 1 x ½ x 2.8 x 4.8 = 13.44m2

Answer: 13.44m2

If you have any questions related to the formula for calculating the area and perimeter of a rhombus, please leave a comment below to discuss and answer together. Thank you for following the article.