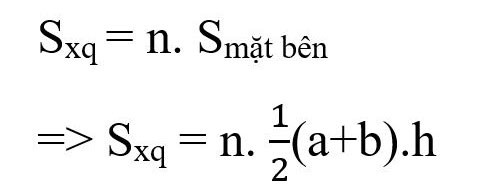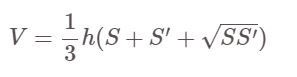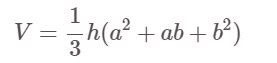Formula for calculating the volume of a truncated pyramid, the lateral area and total area of ​​a truncated pyramid

Let's learn what a truncated pyramid is, how to calculate the volume of a truncated pyramid, the lateral area and total area of ​​a truncated pyramid in the article below.

Table of Contents

• Definition of frustum
  • Properties of truncated pyramid:
• Formula for calculating the area of ​​a truncated pyramid
  • Surface area of ​​truncated pyramid 
  • Total surface area of ​​a truncated pyramid
• Formula for calculating the volume of a truncated pyramid

Definition of frustum

A truncated pyramid is a part of a polyhedron, located between the base and the cross-section cut by a plane parallel to the base of the pyramid.

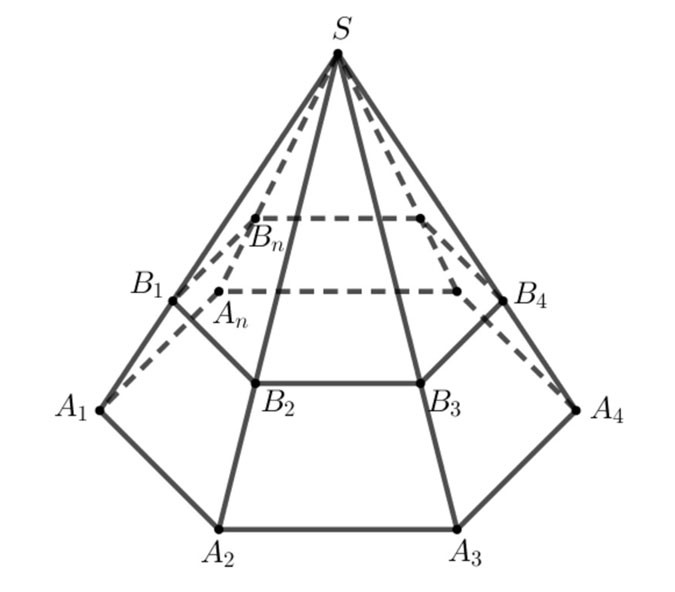
• The figure consisting of polygons A1A2...An,B1B2...BnA1A2...An,B1B2...Bn and trapezoids A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn is called a truncated pyramid, denoted as A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
• Simply put, a truncated pyramid is formed from the pyramid S.A1A2...AnS.A1A2...An after cutting off the pyramid S.B1B2...Bn.S.B1B2...Bn.

+ The polygons A1A2...An,B1B2...BnA1A2...An,B1B2...Bn are called the two bases,

+ Trapezoids A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn are called lateral faces.

+ The line segments A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn are called the side edges, the edges of the base surface are called the base edges.

+ The distance between the two bases is called the height of the truncated pyramid.

Properties of truncated pyramid:

• The two bases are two polygons (triangles, quadrilaterals, pentagons, etc.) with corresponding parallel sides and equal ratios of corresponding sides.
• The side faces are all trapezoids.
• The lines containing the lateral edges will converge at a point (the top of the pyramid).
• A truncated pyramid is a pyramid whose bases are regular polygons (with equal sides). Therefore, the lateral faces of a truncated pyramid are all equal isosceles trapezoids.

Formula for calculating the area of ​​a truncated pyramid

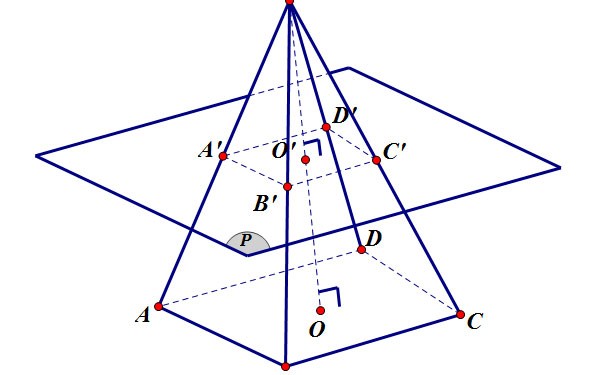
Surface area of ​​truncated pyramid

The lateral area of ​​a truncated pyramid is the area of ​​the surrounding faces, the part surrounding the truncated pyramid, excluding the area of ​​the two bases.

How to calculate the lateral area of ​​a truncated pyramid: Calculate the area of ​​each side face (trapezoids) of the truncated pyramid according to the formula for calculating the area of ​​a normal trapezoid , then calculate the total area.

Formula for calculating the area of ​​a regular truncated pyramid:

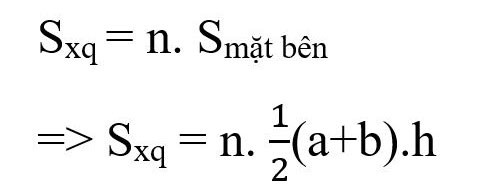
In there:

• Sxq: surrounding area
• n: number of lateral faces of the truncated pyramid (equal to the number of edges of the base polygon)
• a, b: side lengths of the upper and lower bases respectively
• h: height of the side quadrilaterals.

Example 1: 

Calculate the lateral area of ​​a regular quadrilateral truncated pyramid with base edges of 10cm and 15cm and side height of 12cm.

Prize: 

The side face of a regular quadrilateral truncated pyramid is an isosceles trapezoid, so the area of ​​one side face is:

A regular quadrilateral truncated pyramid has 4 equal sides, so its lateral area is:

150 x 4 = 600 (cm2)

Example 2: Calculate the lateral area of ​​a regular quadrilateral truncated pyramid with base edges of 6cm and 8cm and side height of 5cm. Calculate the lateral area of ​​a regular quadrilateral truncated pyramid with base edges of 6cm and 8cm.

Prize: 

The side face of a regular quadrilateral truncated pyramid is an isosceles trapezoid, so the area of ​​one side face is equal to

A regular quadrilateral truncated pyramid has four equal sides so its lateral area is equal to

35 x 4 = 140 (cm2)

Total surface area of ​​a truncated pyramid

The total area of ​​a truncated pyramid is equal to the sum of the lateral area and the area of ​​the two bases.

Formula:                    Stp = Sxq + Big bottom + Small bottom

In there:

• Stp: Total area
• Sxq: Surrounding area
• Large base: Large base area
• Small base: Small base area

For example: 

Calculate the total area of ​​a regular truncated pyramid according to the dimensions given in the figure.

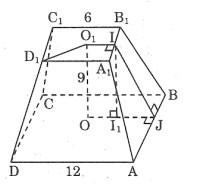
Prize:

We have:

AD = 12 ⇒ OJ = 6

Draw II1 ⊥ OJ we have: I1J = 3

Applying the Pythagorean theorem to right triangle II1J we have:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Hence:

The area of ​​one side of a trapezoid is:

The surrounding area is equal to:

The area of ​​the upper base is: S = 6 x 6 = 36 (units)

The area of ​​the bottom base is: S = 12 x 12 = 144 (units)

The total area of ​​a truncated pyramid is equal to:

Formula for calculating the volume of a truncated pyramid

Recipe:

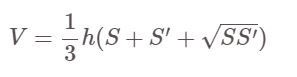
In there:

• V: volume of truncated pyramid
• S, S' are the areas of the large and small bases of the pyramid, respectively.
• h: height of the pyramid, that is the distance between the two large and small bases

Is a truncated pyramid a square (regular quadrilateral):

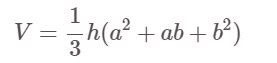
In there:

• V: Volume
• h: Height of the pyramid
• a, b are the lengths of the edges of the large base and the small base respectively.