Formula for calculating height in regular, isosceles, equilateral, and right triangles

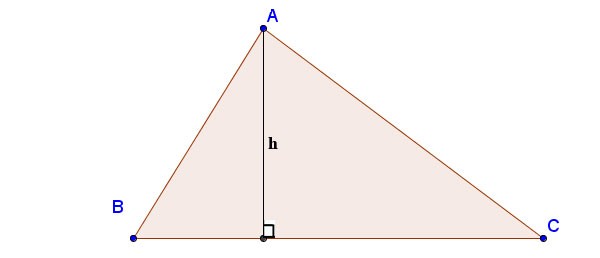
The height of a triangle is an important straight line and is closely related to many plane geometry problems. So what is the height and how to calculate the height of a triangle? Refer to the article below for the answer and the simplest formula for calculating the height of a triangle.

Table of Contents

• Formula for calculating height in a triangle
  • Calculate the height in a regular triangle
  • Calculate the height in an equilateral triangle
  • Formula for calculating height in a right triangle
  • Formula for calculating height in an isosceles triangle
• Definition of altitude in a triangle
• Properties of the three altitudes of a triangle

Formula for calculating height in a triangle

Calculate the height in a regular triangle

How to calculate the height of a triangle using Heron's formula:

With a, b, c being the lengths of the sides; ha being the height drawn from vertex A to side BC; p being the semi-perimeter:

For example: 

Given triangle ABC, side AB = 4 cm, side BC = 7 cm, side AC = 5 cm. Calculate the height AH from A intersecting BC at H and calculate the area of ​​ABC.

Prize:

Half perimeter of triangle: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Height   

=>

Consider triangle ABC, we have:

So,

Calculate the height in an equilateral triangle

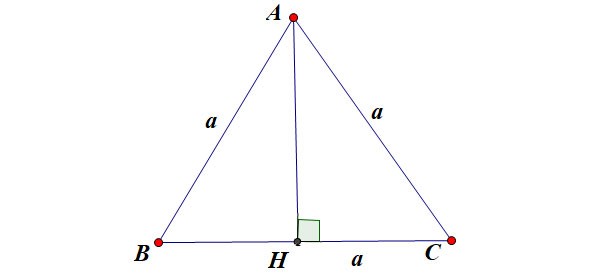
Suppose equilateral triangle ABC has side length a as shown in the figure:

In there:

• h is the height of an equilateral triangle
• a is the side length of an equilateral triangle

Formula for calculating height in a right triangle

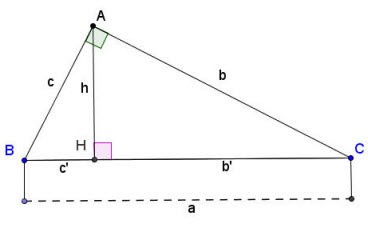
Suppose there is a right triangle ABC right at A as shown above:

Formula for calculating sides and heights in a right triangle:

1. a2 = b2 + c2

2. b2 = ab′ and c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

In there:

• a, b, c are the sides of a right triangle as shown above;
• b' is the projection of edge b onto the hypotenuse;
• c' is the projection of edge c onto the hypotenuse;
• h is the height of a right triangle drawn from the vertex of right angle A down to the hypotenuse BC.

Example 1: Given triangle ABC right angled at A, height AH. Calculate BC, AC, AH knowing AB = 15cm, HC = 16cm.

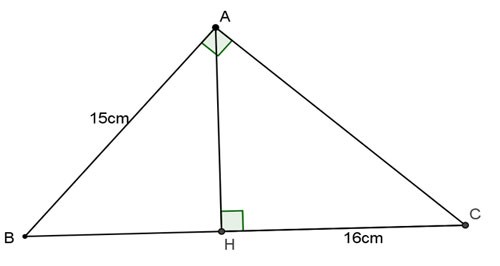
Prize:

Applying the algebraic formula in right triangle ABC we have:

AC2 = CH.BC = 16.BC

According to the Pythagorean theorem for right triangle ABC with right angle A we have:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 or BC = -9 (eliminate)

⇒ AC2 = 16.BC = 16.25 = 400 ⇒ AC = 20 (cm)

Consider right triangle ABC with: AH.BC = AB.AC (geometric formula)

=> AH = AB.AC/BC = 15.20/25 = 12(cm)

So BC=25(cm); AC=20(cm); AH=12(cm)

Example 2 :

Given triangle ABC is right at A, AB=24cm, AC=32cm. The perpendicular bisector of BC intersects AC, BC in order D and E. Calculate DE.

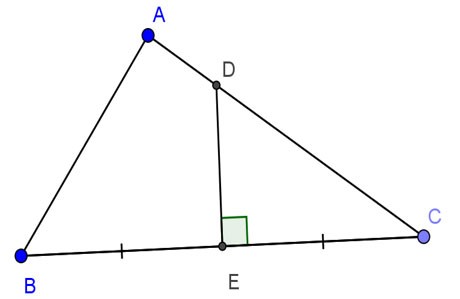
Prize:

Consider right triangle ABC, we have:

BC2 = AB2 + AC2 (according to the Pythagorean theorem)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Consider right triangle ACB and right triangle ECD with:

There is ∠A = ∠E = 90o

∠C common

=> Triangle ACB ∾ triangle ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

So ED = 15cm

Formula for calculating height in an isosceles triangle

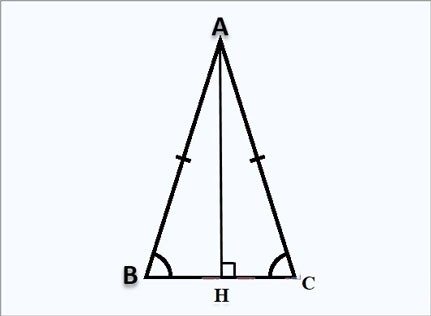
Suppose you have an isosceles triangle ABC at A, the height AH is perpendicular at H as shown above:

Formula for calculating height AH:

Because triangle ABC is isosceles at A, the height AH is also the median, so:

⇒ HB=HC= ½BC

Applying the Pythagorean theorem in right triangle ABH right at H we have:

AH²+BH²=AB²

⇒AH²=AB²−BH²

For example : Given Δ ABC is isosceles at A with BC = 30(cm), height AH = 20(cm). Calculate the height corresponding to the side of that isosceles triangle.

Solution: Consider Δ ABC is isosceles at A with BC = 30(cm)

⇒ BH = CH = 15(cm).

Applying the Pythagorean theorem we have:

Now we have to calculate BK = ?

We have:

On the other hand

Therefore, we have ⇔

Definition of altitude in a triangle

An altitude of a triangle is a perpendicular segment drawn from a vertex to the opposite side. The opposite side is called the base to which the altitude is drawn. The length of the altitude is the distance between the vertex and the base.

Properties of the three altitudes of a triangle

The three altitudes of a triangle pass through the same point. That point is called the orthocenter of the triangle .

You just need to calculate the unknown components in the above formulas for calculating the height of a triangle to be able to calculate the height of a triangle.

• What is the centroid? Formula for calculating the centroid of a triangle