Let's learn and review the formula for calculating the surface area and volume of a sphere with Quantrimang.com in the article below.
Table of Contents
A sphere is the locus of points equidistant from a given fixed point O rin 3-dimensional space. Point O is called the center and the distance ris called the radius of the sphere.
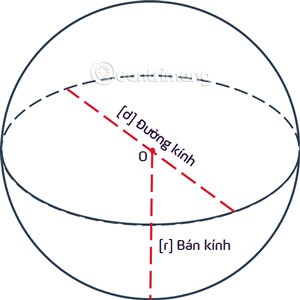
A sphere is a set of points lying inside a sphere and a sphere is called a sphere or sphere with center O and radius r = OA.
The surface area of a sphere is four times the area of a large circle, which is four times the constant Pi multiplied by the square of the radius of the sphere.
The volume of a sphere, also known as the volume of a sphere, is calculated by multiplying three-quarters of Pi by the cube of the radius of the sphere.
In there:
Sis the surface area of the sphereVis the volume of a sphereris the radius of the sphere/spheredis a sphere/sphere
Example : Given pyramid S.ABCD with a rectangular base with AB = 3a, BC = 4a, SA = 12a and SA perpendicular to the base. Calculate the radius R of the sphere circumscribing pyramid S.ABCD.
Solution: We have
So
The square block OABC has OA, OB, OC, perpendicular to each other and has:
For example:
The tetrahedron OABC has OA, OB, OC, mutually perpendicular and has a circumscribed sphere radius of . The largest volume of the tetrahedron OABC
Solution : We have
On the other hand we have:
According to the AM - GM inequality we have:
In there:
Example 1: Given a sphere of radius R circumscribing a cube of side a. Which of the following statements is true?
A.
B.
C.
D.
Solution: We have
So, the answer is C.
The tetrahedron (H1) has vertices that are the vertices of the vertical prism (H2), then:
In which R, d are the radius of the base; a, x are respectively the length of the intersection of the side face and the base, the angle at the top of the side face looking down at the base.
Or you can use the formula
In which: Rb is the circumscribed radius of the side face and a is the length of the intersection of the side face and the base.
For example:
Given pyramid S.ABCD with a square base, equilateral triangle SAD with side √2a and lying in a plane perpendicular to the base. Calculate the radius R of the sphere circumscribing pyramid S.ABCD.
A.
B.
Solution: We have
So the correct answer is B.
Exercise 1 : Given a circle with a circumference of 31.4 cm. Calculate the volume of a sphere with a radius equal to the radius of the given circle.
Prize:
Circumference of circle C = 2πr = 31.4 cm
=> Radius r = C/2π = 5 cm
The volume of the given sphere is:
V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523.3 cm³
Lesson 2 : Calculate the volume of a sphere with diameter d = 4 cm.
Prize:
Radius r = d/2 = 2 cm
The volume of the sphere is:
V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33.49 cm³
Lesson 3 :
Let a circle of diameter 4a rotate around its diameter. What is the volume of the rotating solid?
Solution: Given a circle with diameter 4a rotating around its diameter, we get a sphere with diameter 4a or radius R = 2a.
The volume of the sphere is:
Lesson 4 :
The sphere with radius R√3 has an area of:
A. 4√3πR2
B. 4πR2
C. 6πR2
D. 12πR2
Solution: Apply the formula: S = 4πR2
The surface area of a sphere with radius R√3 is: S = 4π(R√3)2 = 12πR2
So the answer is D.
Two short formulas but it is quite difficult to remember for a long time. Bookmark the article and open it when you need. Hope the article is useful to you.
In addition to the formula for calculating the surface area and volume of a sphere above, you can also refer to the formula for calculating the area of some other basic shapes such as triangles , rectangles , parallelograms ...
The flower of the other shore is a unique flower, carrying many unique meanings. So what is the flower of the other shore, is the flower of the other shore real, what is the meaning and legend of the flower of the other shore?
Craving for snacks but afraid of gaining weight? Dont worry, lets explore together many types of weight loss snacks that are high in fiber, low in calories without making you try to starve yourself.
Prioritizing a consistent sleep schedule and evening routine can help improve the quality of your sleep. Heres what you need to know to stop tossing and turning at night.
Adding a printer to Windows 10 is simple, although the process for wired devices will be different than for wireless devices.
Diet is important to our health. Yet most of our meals are lacking in these six important nutrients.
You want to have a beautiful, shiny, healthy nail quickly. The simple tips for beautiful nails below will be useful for you.
Students need a specific type of laptop for their studies. It should not only be powerful enough to perform well in their chosen major, but also compact and light enough to carry around all day.
Birth defects are something no one wants. Although they cannot be completely prevented, you can take the following steps to reduce the risk of birth defects in your baby.
As you know, RAM is a very important hardware part in a computer, acting as memory to process data and is the factor that determines the speed of a laptop or PC. In the article below, WebTech360 will introduce you to some ways to check for RAM errors using software on Windows.
The automatic home coffee maker is a modern and professional product, bringing you and your family delicious cups of coffee with just a few quick steps.
Smart TVs have really taken the world by storm. With so many great features and the ability to connect to the Internet, technology has changed the way we watch TV.
Refrigerators are familiar appliances in families. Refrigerators usually have 2 compartments, the cool compartment is spacious and has a light that automatically turns on every time the user opens it, while the freezer compartment is narrow and has no light.
Wi-Fi networks are affected by many factors beyond routers, bandwidth, and interference, but there are some smart ways to boost your network.
If you want to go back to stable iOS 16 on your phone, here is the basic guide to uninstall iOS 17 and downgrade from iOS 17 to 16.
Yogurt is a great food. Is it good to eat yogurt every day? What will happen to your body when you eat yogurt every day? Let's find out together!
