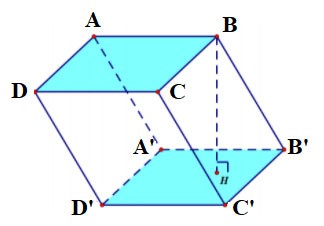
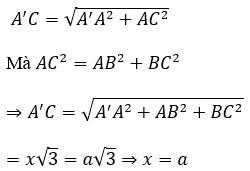A prism is a polygon with two parallel and equal bases and parallelogram side faces.
Comment:
- The lateral faces of a prism are equal and parallel to each other.
- The lateral faces are parallelograms.
- The two bases of a prism are two equal polygons.
What is the formula for calculating the volume of a prism (V prism), the formula for calculating the volume of a vertical prism? Please refer to the article below.
Table of Contents
1. Volume of a vertical prism
Formula for calculating the volume of a vertical prism:
The volume of a right prism is equal to the product of the area of the base multiplied by the height.
In there
Vis the volume of the prism (unit m3)Bis the base area (unit m2)his the height of the prism (unit m)
3. Classification of prisms
Regular prism
It is a vertical prism with a regular polygon base. The lateral faces of the prism are all equal rectangles. For example: a regular triangular prism, a regular quadrilateral... then we understand it as a regular prism.
A regular quadrilateral base is called a regular quadrilateral prism.
Triangular prism
- A triangular prism has 5 faces, 9 edges, and 6 vertices.
- The two bases are both triangular and parallel to each other; Each side face is a rectangle;
- The sides are equal;
- The height of a triangular prism is the length of one side.
For example:
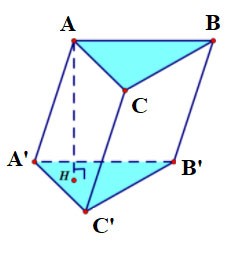
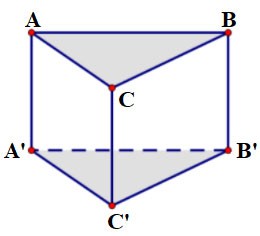
The triangular prism ABC.A'B'C' has:
- The bottom base is triangle ABC, the top base is triangle A'B'C';
The side faces are rectangles: AA'B'B, BB'C'C, CC'A'A;
- Edges:
- Base edges: AB, BC, CA, A'B', B'C', C'A'
- Sides: AA', BB', CC';
- Vertices: A, B, C, A', B', C'.
- Height is the length of one side: AA' or BB' or CC'.
Quadrilateral prism
- A quadrilateral prism has 6 faces, 12 edges, and 8 vertices.
- The two base faces are both quadrilaterals and parallel to each other. Each side face is a rectangle.
- The sides are equal.
- The height of a quadrilateral prism is the length of one side.
For example:
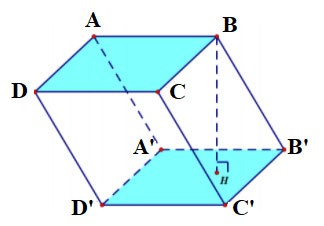
Quadrilateral prism ABCD.A'B'C'D' has:
- The bottom base is quadrilateral ABCD, the top base is quadrilateral A'B'C'D';
The side faces are rectangles: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Edges:
+ Base edges: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Side edges: AA', BB', CC', DD' are equal.
- Vertices: A, B, C, D, A', B', C', D'.
- Height is the length of one side: AA' or BB' or CC' or DD'.
Note: Rectangular prisms and cubes are also quadrilateral prisms.
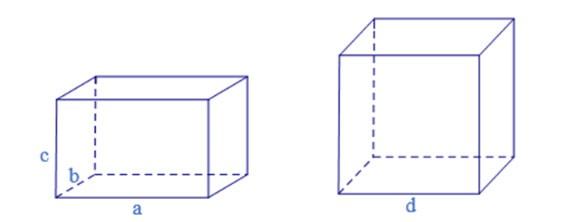
Right prism
If a prism has side edges perpendicular to the base, it is called a right prism.
Note:
If the base is a rectangle, the vertical cylinder of the quadrilateral is called a rectangular box.
If a quadrilateral cylinder has 12 sides of length a, then its name is a cube.
Compare the right prism and the regular prism:
| DEFINE: |
NATURE |
| + A vertical prism is a prism with a side perpendicular to the base. |
+ The side faces of a vertical prism are rectangular.
+ The side faces of the prism are perpendicular to the base face.
+ Height is the side
|
| + A regular prism is a vertical prism whose base is a regular polygon. |
+ The lateral faces of a prism are all equal rectangles.
+ Height is the side
|
4. Example of calculating the volume of a vertical prism
Example 1:
Given prism ABC.A'B'C' with base ABC being an equilateral triangle with side a = 2 cm and height h = 3 cm. Calculate the volume of this prism?
Prize:
Because the base is an equilateral triangle with side a, the area is:
At this time, the volume of the prism is:
Example 2:
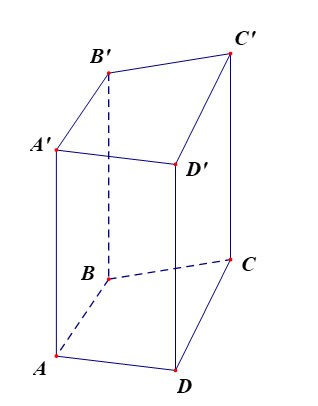
Exercise 1: Given a vertical box with edges AB = 3a, AD = 2a, AA'= 2a. Calculate the volume of block A'.ACD'
Instruct:
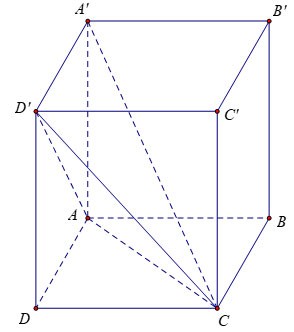
Because the side face ADD'A' is a rectangle, we have:
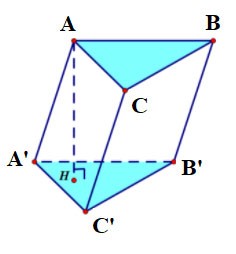
Example 3 : Given a vertical prism ABC.A'B'C' whose base is an equilateral triangle with side a√3, the angle between it and the base is 60º. Let M be the midpoint of BB'. Calculate the volume of the pyramid M.A'B'C'.
Prize:
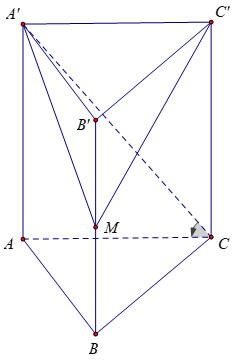
Therefore, we can infer that
We have:
Example 4:
Given a regular quadrilateral prism ABCD.A'B'C'D' with a base edge of a and a face (DBC') with the base ABCD at an angle of 60º. Calculate the volume of prism ABCD.A'B'C'D?
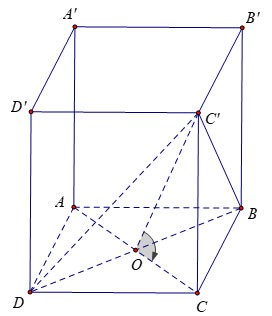
We have: at the center O of square ABCD.
On the other hand therefore
Infer
Also:
Example 5:
Calculate the volume V of cube ABCD.A'B'C'D', knowing AC'=a√3
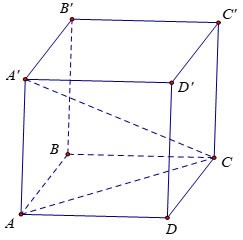
Prize:
Let x be the length of the side of the cube.
Consider triangle AA'C right angled at A with:
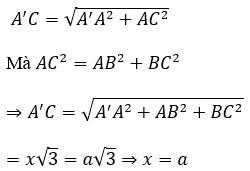
Therefore, the volume of the cube is V=a^3.
In addition to the formula for calculating the volume of a prism above, you can refer to more articles on the formula for calculating the volume of a solid of revolution , the formula for calculating the area and circumference of a circle ...