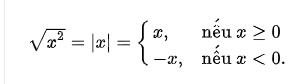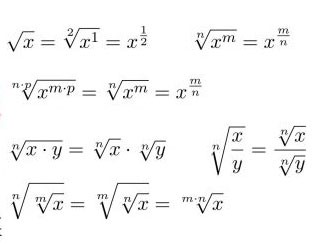Square root, how to calculate square root

Square root is one of the important knowledge in mathematics used throughout the learning process of students. The following article will introduce to you the definition of square root, how to calculate the square root of a number? Please refer to it.

Table of Contents

• What is square root?
• The most basic square root calculations
  • Square root table
• How to calculate square root without using calculator
  • Find the square root of an integer
  • Find the square root of other numbers
• How to compare square roots 

What is square root?

The square root of a number a is a number x such that x2 = a, or in other words, the number x whose squared value = a.

For example, 2 and −2 are square roots of 2 because 2² = (−2)² = 4.

The radical sign is denoted by √.

• Every non-negative real number a has a unique non-negative square root, called the arithmetic quadratic root.

For example, the arithmetic square root of 16 is 4, denoted by √16 = 4, because 4² = 4 × 4 = 16 and 4 is a non-negative number.

Every positive number a has two square roots: √a is the positive square root and −√a is the negative square root. They are both denoted by ± √a.

The most basic square root calculations

Remember some basic and most common square numbers so that when you take square roots, you can calculate faster in your head:

0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289

Some basic square root formulas that everyone should remember include:

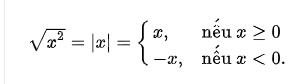
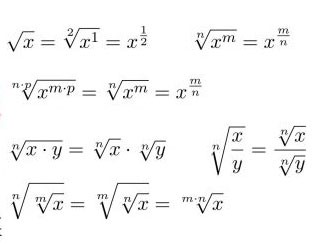
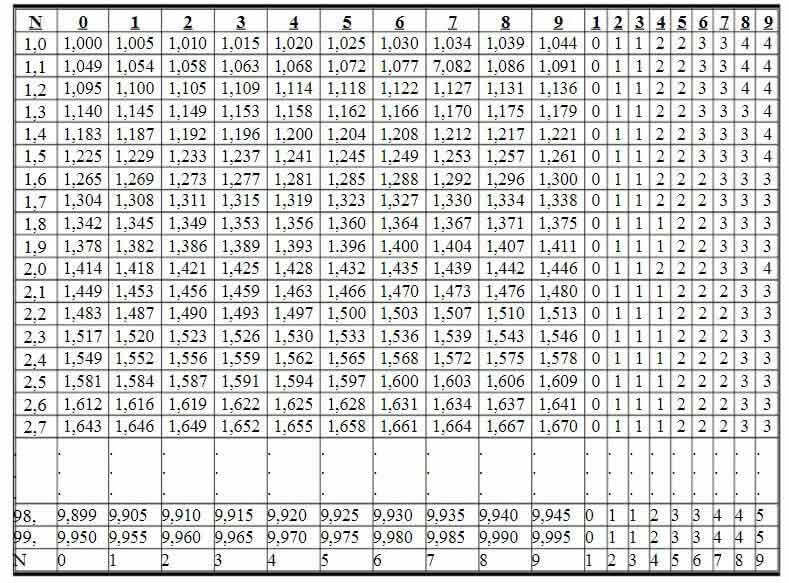
Square root table

The square root table is divided into rows and columns, allowing to directly find the square root of numbers greater than 1 and less than 100.

The square roots of numbers written with no more than three digits from 1.00 to 99.9 are given in the table in columns 0 to 9. Next are nine correction columns used to correct the last digit of the square roots of numbers written with four digits from 1.000 to 99.99.

Example 1: Find

→ Solution:

At the intersection of rows 1,4 and column 1 we see the number 1,187

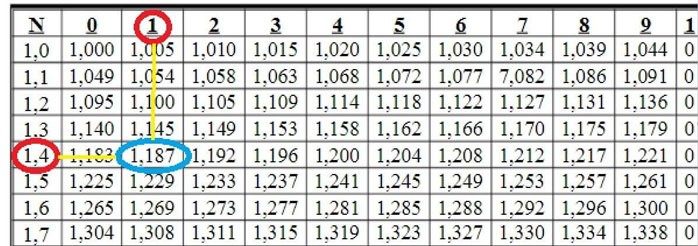
So

Example 2: 

Find

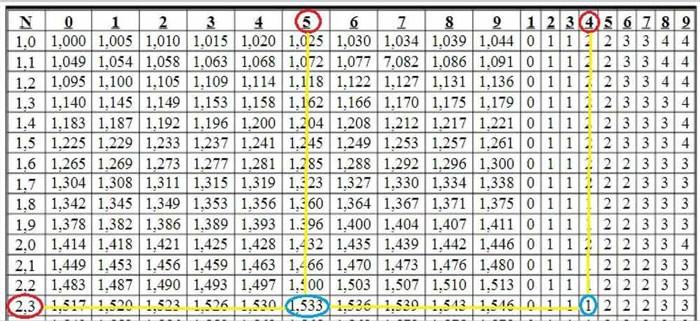
At the intersection of rows 2,3 and column 5 we see the number 1.533. We have

Next, at the intersection of rows 2,3 and column 4, we see the number 1. This number 1 is used to correct the last digit in the number. That is: 1.533 + 0.001 = 1.534

So

How to calculate square root without using calculator

Find the square root of an integer

Find square root by multiplication.

The square root of a number is the number that, when you multiply the number by itself, gives you the original number.

So that means “What number can you multiply by itself to get the number you already have?”

For example:

The square root of 1 is 1 because 1 times 1 equals 1 (1 X 1 = 1).

The square root of 4 is 2 because 2 times 2 equals 4 (2 X 2 = 4).

The square root of 9 is 3 because 3 x 3 = 9.

Use division to find square root

To find the square root of an integer, you can divide the integer by successive numbers until you find a quotient that is exactly the same as your divisor.

For example:

16 divided by 4 is 4 so 4 is the square root of 16.

4 divided by 2 is 2, so 2 is the square root of 4.

Find the square root of other numbers

Guess and then use the process of elimination.

Example: Find the square root of 20.

Meanwhile, we know that 16 is a perfect square number with square root 4 (4X4=16).

25 also has a square root of 5 (5X5=25).

So we would guess that the square root of 20 would be somewhere between 4 and 5.

We can guess the square root of 20 is 4.5 and try squaring 4.5 to check. That is, take 4.5 x 4.5, if the answer is not 20, we will see if the result is greater or less than 20 to calculate. If it is less than 20, we will continue to try with 4.6 and larger numbers. If the result is greater than 20, we will try with 4.4 and smaller numbers until we get the correct result.

The result of this calculation is 4.475 X 4.475 = 20.03. When you round down, the answer is 20.

How to compare square roots

With any 2 positive numbers a and b

If a = b then

If a > b then

If a < b="" then="">

For example: 

Compare and

Because 21 < 31,

Hopefully the above article has helped you grasp the knowledge about square roots, how to calculate, how to compare... to solve exercises about square roots as well as other related exercises.