What is a rational number? What is an irrational number?

Definitions and formulas of rational and irrational numbers are important knowledge in mathematics that students must understand to have a solid foundation in mathematics. The following article introduces to you the definitions, properties, and mathematical forms of rational and irrational numbers. Please refer to it.

Rational numbers, irrational numbers

• What is a rational number?
  • Classification of rational numbers
  • Representing rational numbers on a number line
  • Add and subtract rational numbers
  • Multiply and divide rational numbers
  • Absolute value of a rational number
  • Compare two rational numbers
  • Formula for calculating the power of a rational number
• What is an irrational number?
  • Concept of irrational numbers
  • Properties of irrational numbers
• What is the difference between rational and irrational numbers?
• Relationship of sets of numbers
• Exercises on rational numbers

What is a rational number?

- Rational numbers are the set of numbers that can be written as fractions (quotients). That is, a rational number can be represented by an infinite recurring decimal.

- Rational numbers are written as , where a and b are integers but b must be different from 0.

- is the set of rational numbers.

=> Set of rational numbers: .

For example: , , … are rational numbers.

• Any integer a is a rational number because the integer a can be written in the form .

For example: We have rational numbers.

We have:

Comment: are all rational numbers.

Classification of rational numbers

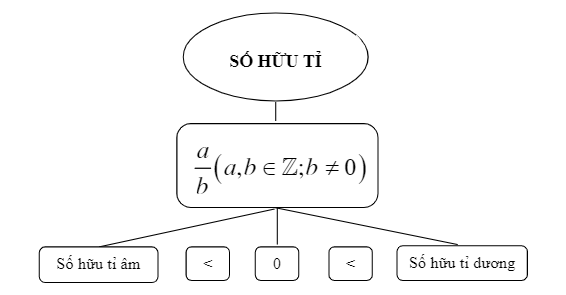
Rational numbers are divided into two types: negative rational numbers and positive rational numbers. Specifically:

• Negative rational numbers: Include rational numbers less than 0.
• Positive rational numbers: Include rational numbers greater than 0.

Note: The number 0 is neither a negative rational number nor a positive rational number.

Nature

• The set of rational numbers is a countable set.
• Commutative property:
• Addition property with 0:
• Combined properties:

Representing rational numbers on a number line

- To represent rational numbers on the number line, we follow these factors:

Step 1: Write the rational number as a fraction

Step 2: Divide the unit line segment into b equal parts to get a new unit segment which is the old unit.

Step 3: The rational number is represented by point A being a distance of a new units from point 0.

• A is to the left of 0 if it is a negative number.
• A is to the right of 0 if it is a positive number.

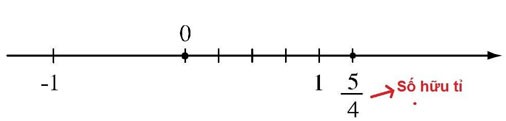
For example: In the figure, point P represents the rational number:

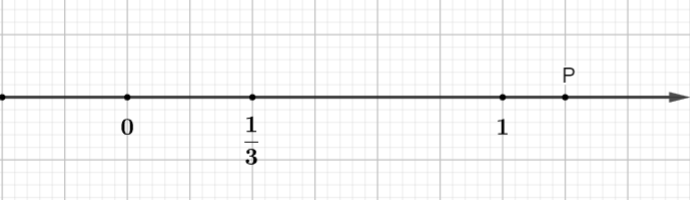
Instruct

The unit line segment is divided into 6 equal parts (new unit is 1/6 of old unit)

Point P is located at a distance of 7 new units from point O.

And point P is to the right of point O so P is a positive rational number.

So P represents a rational number.

Add and subtract rational numbers

i) Rules for adding and subtracting two rational numbers

We can add and subtract two rational numbers x and y by writing them as two fractions and then applying the rules for adding and subtracting fractions.

With us we have:

ii) Properties

- Addition of rational numbers has the properties of addition of fractions: Commutative, associative, addition with 0, addition with opposites.

- We have:

a) Commutative property:

b) Associative properties:

c) Add 0:

d) Add the opposite number:

iii, Transition rules

When moving a term from one side of an equation to the other, we must change the sign of that term.

In Q we have an algebraic sum, in which we can swap terms, put parentheses to group terms arbitrarily like algebraic sums in the set of integers.

• With if then
• With us we have:

Multiply and divide rational numbers

i) Rules for multiplying and dividing two rational numbers

- We can multiply and divide two rational numbers by writing them as fractions and then applying the rules for multiplying and dividing fractions.

• With us we have:
• With us we have:

For example:

Multiply rational numbers: 

Divide rational numbers: 

ii) Properties

- Multiplication of rational numbers also has the same properties as multiplication of fractions: Commutative, associative, multiplication by 1 and distributive property of multiplication over addition.

- Every non-zero rational number has an inverse.

- We have:

• Commutative property: .
• Associative properties: .
• Property of multiplying by 1: .
• Distributive properties: .
• With . The inverse of a is .

Absolute value of a rational number

- The absolute value of a rational number a, denoted by , is the distance from point a to point 0 on the number line.

For example:

(Because )

(Because )

Compare two rational numbers

- With any 2 rational numbers we always have either or or .

- To compare two rational numbers we do the following:

• Write as 2 fractions with the same positive denominator:
• Compare the numerators as integers a, b:

For example: Compare two rational numbers: and

We have:

Because it is good.

Formula for calculating the power of a rational number

Formulas for calculating powers of rational numbers that you need to remember

• Product of two powers with the same base:
• Power of power
• Power of a product
• Power of a quotient

What is an irrational number?

Concept of irrational numbers

• When mentioning rational numbers, one cannot help but mention irrational numbers. These are numbers written in the form of infinite, non-repeating decimals, denoted by .
• Real numbers that are not rational numbers cannot be represented as ratios.

For example: 3.145248… is an irrational number.

Properties of irrational numbers

The set of irrational numbers is an uncountable set.

For example:

Irrational numbers: 0.1010010001000010000010000001… (this is an infinite non-repeating decimal)

Number of square roots: √2 (square root)

Pi (π): 3.14159 26535 89793 23846 26433 83279 50 288…..

What is the difference between rational and irrational numbers?

• Rational numbers include non-terminating recurring decimals, while irrational numbers are non-terminating non-repeating decimals.
• Rational numbers are just fractions, while irrational numbers have many different types of numbers.
• Rational numbers are countable numbers, while irrational numbers are uncountable numbers.

Relationship of sets of numbers

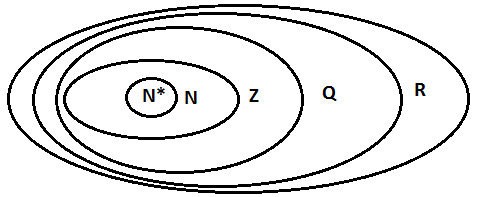
Symbols of sets of numbers:

• N: Set of natural numbers
• N*: Set of natural numbers other than 0
• Z: Set of integers
• Q: The set of rational numbers
• I: Set of irrational numbers

We have: R = Q ∪ I.

Set N; Z; Q; R.

Then the inclusion relationship between the sets of numbers is: N ⊂ Z ⊂ Q ⊂ R

Exercises on rational numbers

Form 1: Perform calculations involving rational numbers

Solution method: To solve exercises on performing calculations related to rational numbers, first convert the rational numbers into fractions, then apply the calculation rules with addition, subtraction, multiplication, and division of rational numbers.

Example: Calculate  

Answer:

Form 2: Representing rational numbers on the number line

Solution: You need to determine whether the rational number is a positive rational number or a negative rational number, then continue with the next steps:

• If the rational number a/b is a positive rational number: On the number line, in the positive direction of the axis, divide the length of 1 unit into b equal parts. Then take a point on the positive direction of the axis Ox, point a part and determine the position of the rational number a/b.
• If the rational number a/b is a negative rational number: On the number line, in the negative direction of the x-axis, divide the length of 1 unit into b equal parts. Then take a point on the negative direction of the Ox-axis, point a part and determine the position of the rational number a/b.

Form 3: Comparing rational numbers

Solution: Convert the given rational numbers into fractions with the same positive denominator, then compare the numerators. At a more advanced level, we can compare with intermediate fractions to find the answer.

Form 4: Determine whether a rational number is negative, positive or 0

Solution method: To solve type 4 exercises, students need to base on the properties of rational numbers to determine whether the rational number is negative, positive or 0.

For example: Given the rational number x = (a – 25)/29, determine the value of a so that:

• x is negative
• x is positive
• x = 0

Answer:

x is a negative number => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x is a positive number => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Form 5: Find rational numbers in the interval according to given conditions

Solution: If the question requires finding rational numbers within an interval according to given conditions, we need to put the rational numbers into the same numerator or denominator to find the answer.

Example: Find the value of m for greater than and less than

Answer guide

Convert fractions to common denominators as follows:

Common denominator: 18

According to the question we have:

Form 6: Find x with rational numbers

Method to solve math problems: For math problems to find x with rational numbers, it is necessary to perform common denominator reduction and convert x to one side, the remaining terms to 1. From there, calculate the value of x.

For example: Find x knowing x . (2/ 3) + 5/ 6 = 1/ 8

Answer:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Form 7: Find a so that the expression is an integer

Method for solving math problems: For the problem of finding a, if the numerator does not contain a, we need to use the divisibility sign. If the numerator contains a, we need to use the divisibility sign or separate the numerator according to the denominator. If the problem requires finding both a and b, we need to group a or b and convert it to fractional form for calculation.

Example: Find the integer a with the condition that 8/(a – 1) is an integer

Answer:

Condition: a – 1 ≠ 0 => a ≠ 1

Let a be an integer => 8 is divisible by (a – 1)

=> (a – 1) is a factor of 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Hopefully the above article has helped you understand what rational numbers are, what irrational numbers are, types of rational numbers, what rational number symbols are, and how to recognize rational numbers to easily solve problems.

In addition to the knowledge about irrational numbers and rational numbers above, you can refer to some other mathematical knowledge such as fractions , mixed numbers , decimals ...